Students often zip through a set of practice problems but then struggle on cumulative exams. What went wrong? Here’s a helpful intervention – and why it may work.
Students often zip through a set of practice problems but then struggle on cumulative exams. What went wrong? Did they forget what they learned? Did they not really understand it? A simple intervention known as interleaved practice can be used in any mathematics course to help students retain the skills they learn and understand when to use them. The intervention requires merely rearranging some practice problems, without creating new material or otherwise altering the course. It can be used in class or at home, with or without computers. It requires little or no professional development, and it’s free. Although the intervention might seem innocuous, it’s backed by science. It has dramatically improved mathematics learning in classroom-based randomized control trials—the gold standard of evidence. Below, we explain what interleaving is, why it works, the evidence for it, and how to use it.
What is interleaving?
Interleaving is simply a way of mixing practice problems in a problem set. Practice problems are interleaved if problems are arranged so that consecutive problems cannot be solved by the same strategy. For example, a probability problem might be followed by a ratio problem. Here’s an illustration:
In contrast, most math assignments are blocked – meaning that they consist of problems that can be solved by the same strategy. For example, a blocked assignment might be devoted entirely to the Pythagorean theorem. Although the problems might demand slightly different tasks – for instance, finding the length of the hypotenuse vs. finding the length of a side – every problem is nonetheless about the Pythagorean theorem:
The intervention
Although most mathematics students typically receive some interleaved practice, often in the form of mixed review assignments before exams, we suggest that a portion of the practice problems in a course be rearranged so that students receive a higher dose of interleaved practice than usual. To be clear, we are not suggesting that students work more problems than they ordinarily do. In other words, the intervention requires only a rearrangement of practice problems – not an increase in the number of practice problems. Here’s a simplified illustration:
Evidence for interleaving
Giving larger doses of interleaved practice is supported by scientific evidence. In several randomized control trials – the gold standard for testing an intervention – students who received mostly interleaved practice scored higher on a final test than students who received mostly blocked practice, even though every student saw the same practice problems.
For instance, we recently conducted a research study in 54 seventh-grade mathematics classes. Each class was randomly assigned to either the mostly-blocked practice group or the mostly-interleaved practice group. Students received practice assignments nearly every week for several months. All students saw the same practice problems, but the problems were either arranged in blocks devoted to a particular concept or interleaved with other problems. After each assignment, teachers presented solutions and required that students correct any mistakes in their work. The practice phase was followed by a review assignment and, one month later, an unannounced test:
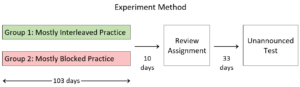
Even though every student practiced the same problems, the test results showed that the mostly-interleaved group outscored the mostly-blocked group by a large margin:
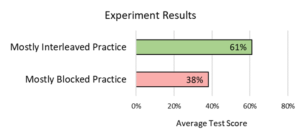
Finally, an anonymous survey completed by the teachers after the study (but before they knew the results of the study or its purpose) showed that nearly all the teachers endorsed interleaved practice.
Why interleaved practice is effective
1) Learning when to use a strategy
To solve a problem, students must first choose an appropriate strategy — often the hardest step. Consider the following problem and the strategies a student might consider:
One reason it’s often hard to choose a strategy is that problems that look alike cannot always be solved by the same strategy. Students face this challenge in every math course from Arithmetic to Calculus:
With a block of problems devoted to a single strategy, such as the Pythagorean theorem, students do not practice choosing an appropriate strategy. Rather, they know the strategy before they read the problem. Thus, blocked practice provides students with a crutch. Students can often zip through blocked practice without understanding why a particular strategy is appropriate, perhaps leading some students (and their teachers) to falsely believe they have mastered the material. This illusion of mastery is often shattered when students encounter a problem on an exam, without the usual cues indicating which strategy is appropriate. In other words, if students don’t learn to solve problems without the crutch of blocked practice, they will struggle during a test when their crutch is taken away.
When practice problems are instead interleaved, students cannot infer the strategy for a problem before they read it. Because consecutive problems require different strategies, students must choose a strategy on the basis of the problem itself – just as they must do when they encounter a problem during a high-stakes test or a subsequent course. Thus, with interleaved practice, students practice choosing a strategy – not just executing a strategy – which helps them understand when to apply the strategy. Furthermore, interleaved practice is a better indicator of whether students have indeed mastered a strategy.
2) Retaining knowledge across time
If you want students to retain a skill they’ve learned, practice of the skill should be distributed, or spaced, across assignments. Indeed, decades of research have demonstrated that spaced practice supports long-term retention. Importantly, a greater degree of interleaved practice ensures a greater degree of spaced practice. Consider a lesson on circumference: Several circumference problems might immediately follow the lesson (blocked practice), but other circumference problems can be mixed into future assignments following other lessons (interleaved practice). Interleaved practice ensures that circumference problems are seen on more days and spread across more assignments than is typically the case – without changing the total number of practice problems. Although students ordinarily receive some degree of spaced practice because of review assignments, replacing some blocked practice with interleaved practice ensures a greater degree of spacing.
The scarcity of interleaved practice in textbooks
Despite its effectiveness, interleaving is underutilized. In most math textbooks, lessons are followed by blocks of problems devoted to that lesson. Even review assignments typically include small blocks of related problems. For example, a chapter review might include a few problems on Lesson 5-1, followed by a few problems on Lesson 5-2, and so forth. These “mini-blocks” again provide a crutch for students.
In one study, we classified every practice problem in six popular U.S. math textbooks for seventh graders, and we found that most problems in each textbook were blocked:
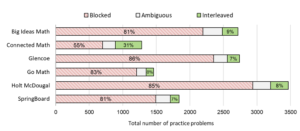
Implementing interleaved practice
Until textbooks, workbooks, and other teaching materials provide more interleaved practice, teachers can create their own interleaved assignments or draw interleaved assignments from other resources. For example:
- Create an interleaved assignment by choosing one problem from each of several blocked assignments in a typical textbook. For instance, the assignment might include p. 37 #19, p. 117 #21, p. 156 #3, and so forth.
- Use the review assignments in a textbook or workbook. Although review assignments often include mini-blocks, these assignments provide at least some interleaved practice.
- Find interleaved worksheets and practice tests on the Internet. For instance, a web search for “mixed review mathematics worksheets” returns a list of websites with freely downloadable interleaved assignments. Also, interleaved practice tests can be found on the websites of companies and organizations that create mathematics assessments.
Some caveats should be kept in mind, however:
- Some blocked practice is probably useful when students first encounter a new concept or skill. Thus, we are not recommending that all practice be interleaved but, rather, that more practice be interleaved. How much interleaved practice is enough? The ideal amount depends on the student and the material, but studies suggest that at least a third of practice problems should be interleaved.
- An interleaved assignment consists of a variety of problem types, including ones not seen recently, so students should have the opportunity to seek help if they’re stuck. This might include asking a teacher for help or having access to lessons or tutorials that explain the concept and provide examples.
- Interleaved practice should be followed by informative feedback. For example, after students have attempted every problem in an assignment, they can be shown the solutions, asked to correct the errors in their work, and given a chance to ask questions. The key point is that students should be encouraged to learn from their mistakes.
- Interleaved practice probably won’t improve performance on a quiz that covers only the last couple days of learning. But short-term learning isn’t the goal of education, anyway. The benefit of interleaved practice is most evident for long-term learning and on cumulative tests.
Takeaway
The bottom line is that interleaved practice boosts test scores without requiring any extra practice. It can be added to any mathematics curriculum by merely rearranging some practice problems. Interleaved practice also makes sense: Students must learn how to both choose and use a strategy. Students must also retain the knowledge across time. Interleaved practice helps students retain the strategies they learn and know when to use them.
Authored by:
Marissa K. Hartwig
Marissa Hartwig received her Ph.D. in experimental psychology from Kent State University. Her research focuses on student learning strategies and metacognition.
Doug Rohrer
Doug Rohrer is a Professor of Psychology at the University of South Florida. He taught high school mathematics before earning his Ph.D. in psychology from the University of California, San Diego. He has conducted numerous studies of learning, especially in mathematics.
Leave a Reply