Taking some key topics, we looked at the relationship between different textbook treatments and student outcomes
The mathematics textbook is the foundation of instruction for most teachers in primary schools. However, knowledge about the role of textbooks for students’ learning is limited, yet at the same time, textbook quality is a construct hard to approach. In our studies, we developed a topic-specific approach towards textbook quality for different features of the arithmetic curriculum. Hence, we were able to show both a measure for the topic-specific textbook quality as well a relationship with the corresponding achievements of students after working with their textbooks.
The textbook is essential for teaching mathematics in most primary schools. It structures the content, serves as a basis for lesson planning, and provides tasks for students and teachers. In the international TIMSS study of 2011, on average 75% of primary schools stated that they use a mathematics textbook as the basis for their lessons. Yet despite intensive use of textbooks in mathematics lessons, the question of what constitutes a “good” textbook is largely unresolved. The consensus is that good textbooks should implement the curriculum content and be free of technical errors. As educational researchers, we are interested in the role of the mathematics textbook as an instrument for teaching and learning mathematics and thus to measure the quality of textbooks by reference to the learning success of the students. Therefore, we conducted four analyses, which together represent the ‘IPN textbook study’ (IPN: Leibniz Institute for Science and Mathematics Education, Kiel, Germany).
Our textbook study
The study was based on longitudinal data of almost 1,700 children from the federal state Schleswig-Holstein, Germany, who were followed from the beginning of primary school to the end of Grade 3. Four different textbook series were used in more than 80 school classes. In the first study, we could show that children differed substantially in the development of their overall arithmetic achievement, depending on which of the four textbooks they used. Of course, there will also be other factors influencing students’ learning. Hence, a number of individual and classroom factors were taken into account in the analysis to guarantee a fair comparison. These include, for example, the students’ abilities at the beginning of primary school (basic cognitive abilities, basic numerical skills and German language skills), the composition of the classes, or whether lessons were held by out-of-field-teachers. The differences in arithmetic performance between the textbook groups were large – comparable to the average learning gain of half a school year.
This first study showed that there are differences between the students’ achievement in arithmetic depending on the textbook used, but not why diffferences exist. To approach this question, we assessed the quality of learning opportunities in textbooks for three arithmetic content areas and were able to show a substantial relation between topic-specific textbook quality and students’ achievement in that topic. In other words, learners in classes using a textbook with higher topic-specific quality also showed a better performance for that topic. The three areas studied were quantitative comparisons and the use of arithmetic principles (each in Grade 1), and adaptive expertise for addition and subtraction in Grade 3. These and the corresponding criteria of textbook quality are presented below.
Quantitative comparisons
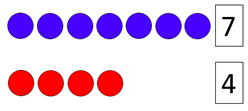
Quantitative comparison problems are one of the four basic situations of addition and subtraction. These are problems such as: “Paul has 4 biscuits, Mila has 7 biscuits, how many more biscuits does Mila have than Paul?”. To generate a viable understanding of operations, children should learn to model different additive and subtractive situations mathematically. Compared to the situations of change (adding/removing), combine or equalise, tasks for quantitative comparison are the most difficult to solve for students. In addition to their static character (which in contrast to dynamic situations does not imply an action), the difficulty of understanding subtraction as a difference has also been cited to explain this. Furthermore, comparison tasks involve linguistic difficulties such as the equivalence of the statements “A has 2 more than B” and “B has 2 less than A”.
Although a varied construction of operational understanding is demanded in curricula, textbooks hardly contain any learning opportunities for quantitative comparisons. Nevertheless, the achievement of students in our sample differs depending on the textbook, even in quantitative comparison tasks. An analysis of these textbooks showed that the following learning opportunities were significant for this.
Criteria of textbook quality
Decomposed numbers with a missing part
Learning opportunities that represent the decomposition of a number with a missing subset should include active (enactive) work assignments as well as pictorial (iconic) and symbolic representations. The three levels should be interlinked, i.e. they should be transferred into each other within a learning opportunity. In addition, learners should be encouraged to exchange about their approaches. These five criteria (three levels of representation, their linking, linguistic impulse) should be taken up on different pages within the textbook, that is, in the instructional part as well as on pages for exercises and repetitions.
Complementarity of addition and subtraction
As with decomposed numbers, the complementarity between the two operations should also be presented using the three levels of representation, these should be linked with each other and the students should be encouraged to exchange linguistically. Here, it makes sense to distribute these criteria throughout the textbook in the form of instruction, exercises and repetition sections, as well.
Subtraction as a difference
The idea of subtraction as a difference should be treated explicitly and complement dynamic subtraction situations, which are often used exclusively. Static representations that enable a one-to-one mapping are useful and thus make the difference set accessible (Fig. 1). Here, too, enactive learning opportunities and symbolic representations should be included and linked to each other. Furthermore, the textbook should provide stimuli for linguistic exchange. As with the previous categories, this should be spread throughout the textbook.
Teacher manual: The teacher manual should include impulses for quantitative comparison. These should be intended for all learners and not only address high-achievers.
Learning opportunities for quantitative comparison
Although the textbooks in our study did not contain explicit learning opportunities for quantitative comparisons, the students’ achievement in our study suggests that such treatment is possible in Grade 1. We assume that such learning opportunities in textbooks are also conducive to students’ learning.
Using Arithmetic principles
The aim of our schools’ first year is for students to replace counting strategies with calculation strategies or the recall of arithmetic problems. This process is long-term and is based on perceiving and using the underlying relationships between numbers and operations. At the core of these relationships are the so-called basic arithmetic principles, which include the commutative equivalent (3 + 4 = 4 + 3), the inversion (e.g. 3 + 4 = 7 > 7 – 4 = 3) and neighbour tasks (e.g. 3 + 4 = 7 > 3 + 5 = 8). In our study, there were clear differences in the students’ use of strategies based on these three principles at the end of Grade 1 – depending on which textbook the students used. The relevant criteria of textbook quality for this topic are based on the model of strategy competence by Robert Siegler and colleagues (Fig. 2).
The following abstraction of these four categories into ‘criteria for textbooks in Grade 1’ showed a significant relation to the students’ use of basic arithmetic principles:Figure 2: Model of strategy competence by Siegler and colleagues
Strategy repertoire
The presentation of the three strategies in different representations is also important here: They should be presented iconically, using educational materials as well as shown in lifelike contexts. Introduction of the strategy names is of importance. Moreover, the execution should be described linguistically. Finally, the representation should be done using manipulatives that are available in the classroom.
Strategy distribution
Multiple presentations of the strategies in a textbook emphasises their importance. The basic arithmetic principles and the corresponding strategies based on them as the core of the relationships of numbers and operations in Grade 1, should therefore not be presented only once. The forms of representation can be varied for repeated presentations.
Strategy efficiency
For the basic arithmetic principles and the corresponding strategies, different problem formats should be included for quick and safe application.
Strategy flexibility
For the flexible application of different strategies, it is important to compare them, which also underlines the possibility of different solution approaches. Also beneficial are structured representations of the basic arithmetic problems, such as in 1+1 or 1-1 tables (Fig. 3), illustrating manifold connections between these problems. In addition, discussions about the suitability of the strategies in concrete situations should be encouraged.
Adaptive expertise for addition and subtraction problems
In Grade 3, we investigated the use of adaptive strategy for addition and subtraction problems up to 1000. Here, too, the school classes showed clear differences in their achievement depending on the textbook used. Since the adaptive use of the relevant addition and subtraction strategies is already dealt with in Grade 2, we examined textbooks for both Grades, 2 and 3.
Four categories of textbook quality were derived from the model of strategy competence (Fig. 1), which turned out to be relevant for students’ adaptive expertise in this topic.
Strategy repertoire
Several strategies should be presented within the textbook. This does not mean that every student should be able to do each strategy. However, a wider range of strategies allows for a choice of different approaches and can better regard individual strengths. The strategies should be introduced as separate learning content (i.e. in the instructional part of a page and not as “math tricks” in the margin) and presented in different forms of representation (e.g., in equation form and on the number line).
Strategy distribution
For an adaptive use of strategies, some of them are more useful than others. The frequency of strategies in the textbook should match this. In particular, strategies should not be presented only once. Learners use strategies more adaptively if they learn different approaches to solving a task early on. Accordingly, textbooks should not emphasise a “main strategy” and refer to other strategies only as “math tricks”.
Strategy efficiency
Increased experience also enhances speed and accuracy in the execution of the different strategies. For this purpose, corresponding problems and tasks must be included to a sufficient extent.
Strategy flexibility
In particular, the comparison of strategies sharpens the view for advantages and disadvantages of the individual strategies. Learning opportunities that demand the comparison of strategies are particularly conducive to an adaptive use of strategies by the learners.
Implications for teachers and school practice
In our studies, we have succeeded in establishing topic-specific criteria of textbook quality, that show a substantial relation with students’ achievement. The textbooks show different strengths and weaknesses depending on the respective topic. On the basis of the criteria presented here, it is not possible to define a global assessment of textbook quality. However, for the three topics studied, these criteria can be applied both in daily teaching and in the selection of a textbook.
Authored by:
Henning Sievert
Henning Sievert is postdoctoral researcher and lecturer of Mathematics Education at Europa-Universität Flensburg, Germany.
Ann-Katrin van den Ham
Ann-Katrin van den Ham is assistant professor of Educational Science, in particular Methods in Empirical Education Research at Hamburg University, Germany.
Aiso Heinze
Aiso Heinze is Professor of Mathematics Education at IPN - Leibniz Institute of Science and Mathematics Education Kiel, Germany.
Leave a Reply